Arboles Binarios

Arboles Binarios

Definición:

Un árbol es una estructura no lineal en la que cada nodo puede apuntar a uno o varios nodos pueden ser estructura no lineal y dinámica de datos. 

Dinámica: puede cambiar durante la ejecución de un programa.

No lineal: a cada elemento del árbol pueden seguirse varios elementos. Están formados por un conjunto de nodos y un conjunto de aristas que conectan pares de nodos.

También se suele dar una definición re cursiva: un árbol es una estructura en compuesta por un dato y varios árboles.

Estas son definiciones simples. Pero las características que implican no lo son tanto.

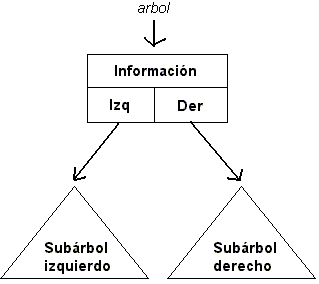
Imagen de  un Árbol Binario

Tipos de Árbol Binario:

• ·         Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.        
•  Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.

•           Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura).

·        A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un árbol binario completo como un árbol binario lleno en el que todas las hojas están a profundidad n o n-1, para alguna n.

Partes de un árbol:

Cuando hay 0 nodos se dice que el árbol está vacío, en caso contrario el árbol consiste en un nodo denominado raíz, el cual tiene 0 o más referencias a otros árboles, conocidos como sub-árboles. 

Las raíces de los sub-árboles se denominan hijos de la raíz

 la raíz se denomina padre de las raíces de sus sub-árboles.

Recorrido de un Árbol:

•  Pre orden: (raíz, izquierdo, derecho). Para recorrer un árbol binario no vacío en pre orden, hay que realizar las siguientes operaciones recursivamente en cada nodo, comenzando con el nodo de raíz:

1. Visite la raíz
2. Atraviese el sub-árbol izquierdo
3. Atraviese el sub-árbol derecho

• In orden: (izquierdo, raíz, derecho). Para recorrer un árbol binario no vacío en in orden (simétrico), hay que realizar las siguientes operaciones recursivamente en cada nodo:

 
1. Atraviese el sub-árbol izquierdo
2. Visite la raíz
3. Atraviese el sub-árbol derecho

• Post orden: (izquierdo, derecho, raíz). Para recorrer un árbol binario no vacío en post orden, hay que realizar las siguientes operaciones recursivamente en cada nodo:

1. Atraviese el sub-árbol izquierdo
2. Atraviese el sub-árbol derecho
3. Visite la raíz

Ejemplo Explicativo de como Recorrer un Árbol Binario:

• Secuencia de recorrido de pre orden: F, B, A, D, C, E, G, I, H (raíz, izquierda, derecha)

• Secuencia de recorrido de in orden: A, B, C, D, E, F, G, H, I (izquierda, raíz, derecha); note cómo esto produce una secuencia ordenada

• Secuencia de recorrido de post orden: A, C, E, D, B, H, I, G, F (izquierda, derecha, raíz)

Declarar un Árbol Binario:

Para implementar el árbol, se utilizan variables de tipo puntero y variables referenciadas.

La variable de tipo puntero se llamará Puntero y apuntará a la variable referenciada Arbol que será un registro que estará formado por tres campos: 

Nodo para almacenar la información sobre el hecho histórico. Rama Izquierda que apuntará al personaje histórico que cumple con las exigencias de la información y Rama Derecha que utilizaremos para apuntar al personaje que no cumple los requisitos de la información.

Type

Puntero = ˆ Arbol;

Arbol = Record

Nodo : String;

RamaIzquierda : Puntero;

RamaDerecha : Puntero;

End;

La variable referenciada se crea dinámicamente utilizando el procedimiento estándar New.

El árbol se construirá creando cada nodo y enlazándolo, después que se creen los subárboles, a su sucesor izquierdo y derecho respectivamente. Para ello se declaran las variables de tipo Puntero:

Var

Elemento, Predecesor : Puntero;

Elemento para el nodo que se crea y Predecesor para poder actualizar los punteros, de ese elemento que se creó, después que se creen los sub-árboles ya que dichos punteros, inicialmente, apuntarán a Nil para indicar que están vacío.

New (Elemento);

Elemento.Nodo := ‘¿Fue asaltante del Moncada?’;

Elemento.RamaIzquierda := Nil;

ElementoRamaDerecha := Nil;

Predecesor := Elemento;

New (Elemento);

Elemento.Nodo := ‘Fidel’;

Elemento.RamaIzquierda := Nil;

ElementoRamaDerecha := Nil;

Predecesor.RamaIzquierda := Elemento;

New (Elemento);

Elemento.Nodo := ‘Martí’;

Elemento.RamaIzquierda := Nil;

ElementoRamaDerecha := Nil;

Predecesor.RamaDerecha := Elemento;

Si al correr el programa el usuario pensó por ejemplo en Maceo, se recorrerá el subárbol derecho al responderse que no fue asaltante al Moncada y se preguntará entonces si es Martí, como la respuesta es de nuevo negativa, le pedirá al usuario que introduzca el nombre del personaje y una información que lo distinga de Martí.

Conclusión: Podemos concluir que los árboles en Object Pascal, permite la representación de estructuras de datos en la memoria de la computadora cuando la relación entre los elementos que componen dicha estructura es una relación jerárquica.

Vídeo: Recorrido En Arboles Binarios:

Ismael Pestana.

Listas

Luis Manrrique                                                                           
                                                                     

       LISTAS

Es una colección de elementos homogéneos entre los que existe una relación lineal.

1.     Cada elemento de la lista, a excepción del primero, tiene un único predecesor

2.    Cada elemento de la lista, a excepción del último, tiene un sucesor

      En una lista cada elemento apunta al siguiente excepto el último que no tiene sucesor. Por ello los elementos son registros  que contienen el dato a almacenar y un enlace al siguiente elemento. Los elementos de una lista, suelen recibir también el nombre de nodos de la lista.                                                                                                                                                                                                                                                              

     TIPOS DE LISTAS                                                                                                                                    

        -Listas Enlazadas

Es una colección de elementos o nodos, en donde cada uno contiene datos y un enlace o liga.

-Listas Lineales

En una estructura lineal los elementos, tiene  una relación 1 a 1. Una lista con nodo de cabecera es aquella en la que el primer nodo de la lista contendrá en su campo algún valor que lo diferencie de los demás nodos :*,-,+, etc.

-Listas Dobles 

Una lista doble o doblemente ligada es una colección de nodos en la cual cada nodo tiene dos punteros, uno de ellos apuntando a su predecesor y otro a su sucesor. Por medio de e estos punteros se podrá avanzar o retroceder a través de la lista, según se tomen las direcciones de uno u otro puntero

-Listas Circulares

La lista circular tiene la característica de que el último elemento siempre apunta al primero.

Sintaxis para crear una lista en pascal

En toda creación de una lista existen dos pasos:

  a)Creación del primer nodo

  b)Creación del resto de los nodos

a)Creación del primer nodo

   new(lista);

   lista^_nodo:=1;

   lista^.siguiente=nil;.

b)Creación de una lista con N nodos

begin

new(lista);

lista^_info:=1;

aux=lista;

for i=1 to N do

begin

new(aux^.sig);

aux=aux^.sig;

aux^.info:I;

end;

aux^.sig=nil;

end;

Operaciones básicas de las listas

Insertar:

Consiste en la introducción de un nuevo elemento en la lista. 

En una lista no ordenada no es necesario mantener ningún orden, por lo tanto, la inserción de los elementos se pueden realizar en cualquier lugar de la lista,al principio, al final, en una posición aleatoria.

Borrar :

Esta operación consiste en la eliminación de la lista de un elemento concreto.

La eliminación de una lista no conlleva ningún trabajo adicional mas que el propio de la eliminación del elemento en si.Para borrar un elemento cualquiera habría que realizar un recorrido secuencial dela lista hasta encontrar el nodo y una vez localizado reestructurar los punteros para saltarse el nodo a borrar y así poder eliminarlo.

Vídeo Relacionado;

   

Nodos

Luis Mojica

Nodos

Cualquier variable que se guarde en memoria, consta de dos partes: la dirección de la celda en memoria, y el contenido de la celda de memoria. Cuando manejamos una variable simple en Pascal, solamente vemos el contenido. El compilador hace transparente todo lo relacionado con la dirección de memoria. Lo que sucede internamente es que, al declarar la variable, por ejemplo a :integer; el compilador reserva una dirección de memoria. Cada vez que hacemos referencia a la variable, por ejemplo, a:=a+1; el compilador traduce la dirección para saber a qué celda de memoria le incrementará el valor.

Sin embargo, es posible el que nosotros manipulemos estas direcciones de memoria directamente. Para ello, utilizamos apuntadores a memoria.

¿Cómo declarar un nodo?

Para declarar un nodo en Pascal, es necesario definir un tipo de dato especial, en el que se incluya la información y el apuntador al nodo.

Ejemplo

TYPE

apunt=^nodo; { aquí defino el apuntador al nodo }

nodo=RECORD { aquí defino el tipo nodo, que incluye un dato y el apuntador al siguiente nodo}

info:INTEGER;

sig:apunt;

END;

VAR

p,q : apunt; { aquí defino dos nodos de tipo apunt }

Ejemplo 2

Escribir un nodo que almacene los datos de un estudiante: cedula nombre numero de carnet, carrera que estudia.

Type

Nodo_estudiante=^tipo_nodo_estudiante ;

tipo_nodo_estudiante=RECORD

CI_estud:STRING[15];

Nom_est:STRING[30];

Carn_est:STRING[10];

Carr_est:STRING[15];

Sig:Nodo_estudiante;

End;

Var

P:Nodo_estudiante;